We need to talk about “old math” vs. “new math” for a hot second. “New math”, in fact, does not exist. Math is math. It has always been the same. Education has just progressed to the point where teachers now realize that problem solving in math is not one size fits all.
For the most part, no single method will resonate with each student in the same way. The three main learning styles (auditory, visual, and kinesthetic) play a large role in this. Because of these different learning styles, it is imperative that teachers find different ways to explain new math concepts.
Problem Solving in Math Is Not One Size Fits All
When I was a student teacher, I was introduced to tape diagrams. This was not something I was familiar with AT ALL and it was a huge learning curve, to say the least. Once I realized how helpful these tape diagrams were to many of my students, I knew how important it was to teach concepts and problem solving in math in different ways.
I carried these same strategies with me to my high school classes. Let me give you a few examples of how I teach polynomial operations in my Algebra 1 classes.
Subtracting Polynomials
Split and Distribute (Horizontal Method)
Stack and Subtract (Vertical Method)
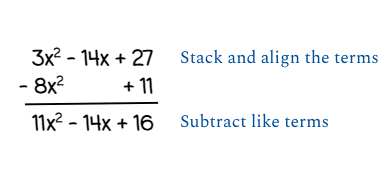
The first way that I teach subtracting polynomials is by using the split and distribute method. Instead of using subtraction, the students will distribute the negative sign and combine like terms like they would with adding polynomials.
For more visual learners, stacking and organizing the polynomials makes it easy to subtract the like terms. Either method a student chooses to solve this problem, they will get to the right answer.
Multiplying Polynomials
Double Distribution
Box Method
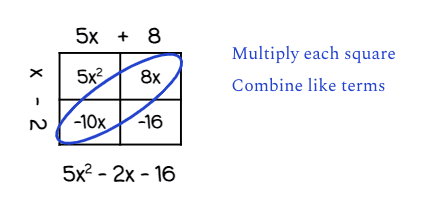
The first strategy uses double distribution (aka the FOIL method) and streamlines the multiplication process. This problem solving strategy is great for students who have a solid understanding of polynomial operations.
The box method is ideal for students who struggle with conceptualizing the solving process and tend to forget steps. It is a visual way for students to make sure they have multiplied all of the terms and solved the problem completely.
Both of these strategies break down the standard algorithm of performing polynomial operations and allow the students to choose what method makes the most sense to them.
In the end, it doesn’t make a difference which way a problem is solved. More importantly, the students should be given the opportunity to choose what makes the most sense to them.
Sure we can teach our students the “old” way to multiply, but do they actually understand where the new numbers are coming from when we do that? With technology advancing as much as it is, math is moving towards why based instruction instead of how.
Pingback: Before You Assign Math Homework, Ask These 3 Essential Questions